In the early days, the series heater arrangement came about to permit operation from DC mains, since transformer type power supplies are suitable for AC only. However, the scheme remained in use even when DC mains were no more. The main reason was that it eliminated the heavy, bulky, and expensive power transformer. This convenience comes at a disadvantage, with the internal circuitry, and usually also the chassis, connected to one side of the mains, making it a shock hazard. Some apparatus was better than others, in regard to avoiding a shock hazard to the user.

Methods for voltage dropping.
Where the sum of valve heater voltages adds up to less than the mains voltage, the difference has to be dropped by some means. Methods to do this include resistors, barretters, light bulbs, or when the supply is AC only, capacitors, diodes, or transformers. Resistive devices are cheap and popular, as well as functioning on both AC or DC mains. They can be in the form of an ordinary wirewound resistor, a barretter, light bulb, ballast tube, or a line cord resistor. The disadvantage is that all the voltage dropped is converted to heat. 30W is not atypical of the sort of dissipation. The overall power consumption is also higher than if a power transformer was/could be used. When the mains is AC only, other more efficient methods can be used. One well known method is to use the reactance of a capacitor. The advantage here is no heat dissipated. Another method, very popular in UK made television sets, is to use a silicon diode, presenting a half wave current to the valve heaters. By using a diode this way, the dissipation in the heater dropper resistor is reduced, because the diode only conducts on every half cycle of the mains sine wave.  Of course a transformer can be used, which may be an auto transformer to reduce bulk and expense, where isolation is not required.

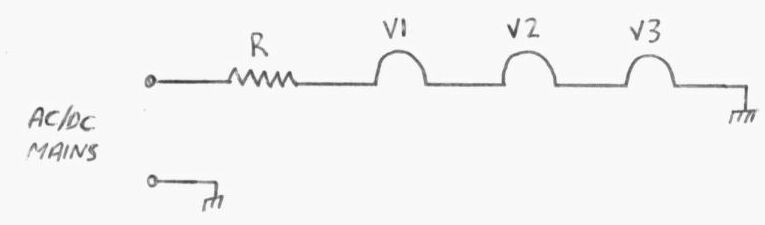
Here, R is any of the resistive devices listed above. The value is found by ohms law where R=V/I. V is the sum of valve heater voltages. For example, lets assume the set uses a 14F8, 12AT6, and 35W4 and is to operate from 120V mains. The sum of heater voltages is 60.2. Now, the voltage to be dropped (V) is 120 - 60.2 =  59.8V. The current consumption (I) is 150mA. So, R= 59.8/.15 or 399 ohms. The power dissipated by this resistor is I^2*R. So, .15^2/399 =  8.98W.
Where an ordinary resistor is used and it fails, it's easy enough to use a modern replacement, using resistors in series or parallel to get the correct resistance, which is critical and should not automatically be substituted with the nearest preferred value.
Many circuits include a negative temperature coefficient (NTC) thermistor in series with the dropper resistor. The purpose of this is to remove the switch on surge current that occurs when the valve heaters are cold. As current flows, the thermistor gradually warms up, because of the voltage drop across it. The resistance then starts to fall to a certain point, at which the full heater current flows.
Where a thermistor is not used, it is worth noting that the lesser the value of dropper resistance, the greater the switch on surge. It goes to reason, for example, that if the dropper was 240 ohms, it would be impossible for more than 1A to flow with a 240V supply. If, however, the dropper was only 120 ohms, then the surge could be as high as 2A.

Big green resistor drops the mains voltage for the valve heaters.

Barretters were popular in Australian and European AC/DC or DC only sets. These resemble a domestic light bulb, but have an iron filament in a hydrogen atmosphere. Usually, they have an E27 Edison screw or P base. Unlike a resistor or light bulb, they regulate the current over a wide mains voltage. So, a typical set could run from 200-250V with no need to adjust anything. Also, the switch on surge is reduced. It would be possible to use an ordinary light bulb and forego the regulation feature as a replacement, but more than likely, it will be necessary to provide a resistor as well, to get the correct heater current. Barretters are fragile, and must be mounted away from speaker magnets, since the iron filament will vibrate with the magnetic field and eventually break.

Type 302 barretter is at the right.

Ballast tubes existed in some American sets from around the 1930's and 40's. One kind is a wirewound resistor assembled in what looks like a perforated metal valve, and has an ordinary valve base. It may be possible to fit modern resistors inside the enclosure. Even if not, they could be put elsewhere inside the set, above the chassis. The other kind of ballast tube is in a glass envelope, and is really a barretter under another name.

Light Bulbs can and have been used, but resistance varies depending on the current flow, so it isn't practical to calculate what wattage lamp is to be used, and what the associated resistor (if required) will be. It will have to be done experimentally. As a starting point, it is easy to determine what the current consumption of a light bulb at its rated voltage is. P(power of lamp) = I(current) x V(voltage). For example, a 240V 60W bulb draws about 250mA. A 75W 240V bulb would probably be a good starting point for use in a set that had a 300mA heater string (You have hoarded a lifetime supply of incandescent bulbs haven't you? Because you won't be able to use a CFL or LED bulb in this application!). Keep in mind that the resistance of a light bulb is much lower cold than hot, so the switch on surge could be a problem. A thermistor could be of use here.
Ordinary light bulbs have a tungsten filament, so have the same temperature coefficient as a string of valve heaters. Interestingly, a carbon filament bulb performs much like a negative coefficient thermistor. This data was measured using two 240V 100W bulbs; one with a tungsten filament, and the other with a carbon filament:
 

Volts across bulb	Carbon filament (mA)	Tungsten filament (mA)
40	45	155
80	110	230
115	170	270
140	235	310
180	320	360
215	395	390
240	415	420
Cold resistance	786 ohms	40.6 ohms

Characteristics of 240V 100W carbon and tungsten filament bulbs.

From this, one could deduce that the carbon filament provides good inrush current protection, with such a high cold resistance. However it does not provide current regulation like a barretter, so is unsuitable for operating over a wide voltage range. As mains voltages have been standardised for some time, this is not as important as it once was. The tungsten lamp has less of a current variation over a certain voltage range, but offers no surge protection at all. The effect of using a tungsten lamp as a valve heater dropper is the same as if all the valve heaters added up to the mains voltage. For example, if the mains voltage rises 10%, then each of the valve heater voltages rises by 10%.
In comparison, an ordinary wirewound resistor does offer useful surge protection, but as the resistance does not vary with current, the valve heaters will be subjected to a greater variation in voltage than with a tungsten lamp dropper.
For these reasons it can be seen that the barretter is actually the ideal type of resistive dropper.

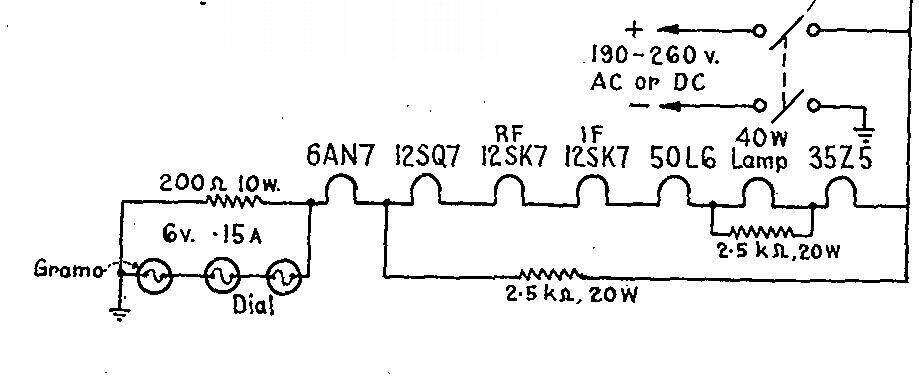
40W light bulb used in the Operatic C64RC.

A domestic 240V 40W light bulb was used in the Operatic C64RC as the dropper. Service notes indicate that it was used due to barretters being in short supply. Because the bulb current is too low on its own, it has a 2.5k resistor shunted across it. The next size bulb up, 60W, passes too much current. The section of the heater string comprising the 12SQ7,the 12SK7's, 50L6, and 35Z5 draws 150mA. Since the 6AN7 requires 230mA, the 150mA section is shunted by another 2.5k resistor.

Line cord resistors took over from ballast tubes and other dropper resistors mounted inside radio cabinets, and lasted until the 1950's when they fell from use. By then, a series of valves had been developed for typical radio use which had 150mA heaters, and when used together added up to around 122V, thus dispensing with the need for any dropper for the U.S. mains supply. Line cord resistors were not used with Australian sets due to their safety hazards, and were not permitted by the authorities.
The reason for their popularity is that they allowed midget sets to be constructed, as all the heater dropper heat was dissipated outside the cabinet. Room was also not required inside the set for the large resistor or ballast tube.
A line cord resistor looks like an ordinary cloth covered appliance cord, but closer examination reveals three conductors. There are two ordinary conductors, one for (what is hopefully) the neutral, the other to feed the rectifier plate with the mains voltage. The third conductor is actually resistance wire wound around the length of the cord and provides the heater voltage. Needless to say, shortening this kind of cord will subject the heaters to excessive voltage. Provided the cord is left stretched out, it dissipates the heat effectively. If left coiled up, it could be a fire hazard.
The insulation around the resistance wire is unreliable making them a shock hazard. Also, the resistance wire is not as flexible as the ordinary conductors. So, continual rolling up or moving the cord will eventually cause it to break. It's the usual cause of no heaters lighting in a set fitted with one.

Construction of a line cord resistor. The red and black conductors connect to the mains plug and thus provide full voltage to the B+ rectifier. Wound around the black conductor can be seen the nichrome resistance wire
for dropping the voltage for the valve heaters. With nothing but a woven cotton outer covering, the shock hazard is obvious.

And so to the Line Cord Resistor Replacement:
Line cord resistors have not been made for many years, and with today's regulations, probably never will be again. Faced with an open circuit line cord, many restorers have resorted to other types of dropper, which apart from detracting from originality, can present its own challenges. Replacing a line cord with an ordinary resistor is often not practical because the set's cabinet is too small to accomodate it, and the resulting heat dissipation will cause damage. Sometimes the resistor has been installed in an external metal box, which obviously stands out like the proverbial.

Some restorers use capacitive droppers which have the advantage of no heat dissipation, and provided there is enough room in the cabinet are a practical alternative. However, many restorers make the error of simply calculating the capacitor value by the equivalent reactance, which overloads the valve heaters. There are limitiations of this type of dropper which need to be understood before choosing it. The details of how to design a capacitive dropper circuit are covered in Part 2.

Diode droppers also take up little space, but for most applications a dropper resistor is still required. Nevertheless, the size of resistor and its heat dissipation is a lot less than a resistor on its own. Again, the calculations are often done in error, assuming the voltage is simply halved, with the valves being overloaded. The details are covered in Part 3.

A transformer in an external box is another option, but again looks out of place. Once in a while, there is just enough room to install a small heater transformer inside the set, as was done with this Meck FM converter.

Since only 12.6V at 300mA was required, there was enough room to fit this heater transformer in a Meck FM converter.

However, it occurred to me that it should be possible to make a replacement using wire from an electric blanket heating element. This has the required insulation (in fact, much better than what was originally used), and flexibility requirements (again, vastly improved on the original). By shrouding it in hollow shoe lace along with two ordinary conductors, it should therefore be possible to make an authentic replacement. Indeed, it turned out that electric blanket element wire also had the right electrical characteristics, and the idea has been successfully implemented on two receivers so far.

Reproduction line cord resistor made for an Emerson CF255.

Thus, there is no need to butcher the original radio with non original droppers.
The first reproduction line cord resistor was used on one of my Meck FM converters. See the full description here.
The second was made for one of my Emerson CF255's. This set requires a tap for the dial lamp, but this was easily provided.

• How to make a line cord resistor.

Transformers.
No introduction needed here. Efficiency is high, and there's no asymmetrical loading of the mains or reducing the power factor. Not frequency critical within limits either. As we're talking about live chassis sets here, an auto transformer can also be used. Obviously, a transformer is the best way to power the heaters when practical. Of course, transformers are suitable only for AC supplies.

• Go to Part 2: Capacitive Droppers >